Último Ás
Imagine que você chega a um cassino e é convidado a jogar um novo jogo. Talvez não seja o mais interessante, mas aqui estão suas regras: o dealer pega o baralho e começa a virar as cartas uma por uma, e você deve adivinhar quando o último Ás do baralho aparecerá. Talvez a carta 25 ou 38 – você pode indicar qualquer posição. O baralho é bem misturado e a distribuição das cartas é aleatória. Adivinhar corretamente o último Ás paga o mesmo, independentemente da posição escolhida.
Parece difícil encontrar uma estratégia vencedora para um jogo como este, já que os ases podem terminar em qualquer lugar num baralho como este. No entanto, na realidade, temos uma escolha ótima que irá maximizar as nossas hipóteses de ganhar. Esta escolha é
Spoiler:
A última, a 52ª carta do baralho.
Ao escolhê-la, você ganhará cem por cento das vezes.

Estou brincando, é claro. Você simplesmente ganhará com mais frequência do que com qualquer outra resposta. Vamos descobrir o porquê.
Em primeiro lugar, existem respostas obviamente estúpidas neste jogo. Não faz sentido escolher as três primeiras cartas porque isso, por definição, é impossível. Mesmo que esta carta seja um ás, definitivamente não será a última do baralho. O ás que precisamos poderia, teoricamente, sair em algum lugar entre a 4ª e a 52ª carta.
Digamos que você escolheu a 38ª carta. Em quatro dos 52 casos, você verá um ás, mas a probabilidade de que seja o último ás do baralho não é de cem por cento. Uma diferença importante na escolha da 52ª carta é que ao pegar ela, você garante que o ás que sair nesta posição será o último.
Para entender melhor por que isso é importante, vamos jogar com um baralho de seis cartas.

O objetivo de aproximar a escolha do final do baralho é que quanto mais avançamos, maior a chance de a carta que escolhemos ser o quarto e último ás. Ao escolher a quarta carta, ganhamos apenas se os três ases anteriores estivessem nas primeiras posições. Este não é estritamente um cenário único, pois não levamos em consideração os naipes. Nossos ases podem sair em qualquer ordem, então temos 24 mãos vencedoras.
Mas quando escolhemos a quinta carta, precisamos de mais cenários. Os Ases podem ser embaralhados da mesma maneira, mas qualquer posição antes deles ou entre eles também pode incluir qualquer uma das duas damas. E haverá ainda mais opções para a nossa vitória na escolha da sexta carta.
Não quero mergulhar em cálculos de 52 cartas. Aqui, por exemplo, estão todos os cenários de um baralho de três cartas – com dois ases e um rei.

Obviamente, não adianta escolher a primeira carta – nunca venceremos. A escolha da segunda carta nos trará a vitória em dois dos seis casos. A escolha da terceira carta ocorre em quatro casos entre seis. A conclusão é óbvia!
Curinga no Poker
Para compreender as condições deste problema, basta saber como é determinada a força da mão no poker. Abaixo, organizei todas as combinações por classificação, da carta alta até o royal flush.

Como a maioria de vocês sabe, a força de uma combinação é determinada pela probabilidade de sua ocorrência: quanto menos frequente ela ocorrer, mais forte ela será. Existem apenas quatro royal flushes, 36 straight flushes, 624 combinações de quadra e assim por diante. O número total de combinações ultrapassa 2,5 milhões.
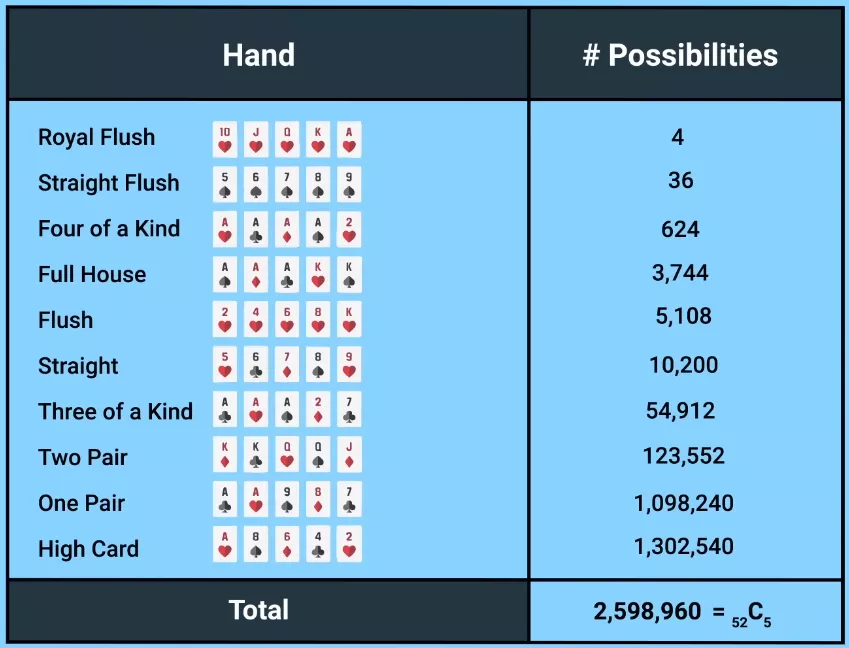
Vamos imaginar que adicionamos um curinga ao baralho. O baralho agora tem 53 cartas em vez de 52. Depois de receber um curinga, você pode transformá-lo em absolutamente qualquer carta. Claro, você tentará fortalecer sua combinação tanto quanto possível. Mão sem curinga – é apenas um par. Com um curinga – é uma trinca se o transformarmos em . Transformando o curinga em também fortalece a nossa mão, mas apenas até dois pares; mas nós, é claro, escolhemos uma combinação mais forte.
E agora minha pergunta:
A classificação das combinações deveria mudar quando jogamos com um curinga e, em caso afirmativo, como exatamente?
Talvez ter um curinga no baralho torne um flush menos provável do que um full house? Talvez haja outras mudanças? Uma coisa pode ser dita desde já: a combinação de “cinco cartas idênticas” aparece com o curinga. Que lugar na hierarquia ela ocupará?
Obviamente, a primeira: o número de combinações é igual ao número de valores das cartas do baralho, 13. Existem seis vezes mais royal flushes com curingas, e com 24 combinações, elas caem para o segundo lugar.

Mas não teremos outros novos tipos de mãos. Então, a classificação das combinações mudará por causa do curinga ou não?
Espero que você tenha tido tempo para pensar sobre esta questão porque agora vou lhe dizer a resposta:
Spoiler :
Ao jogar poker com um curinga, não há como classificar as combinações de acordo com a probabilidade de sua ocorrência.
Por que isso? Por causa do paradoxo associado às trincas e dois pares.
Suponhamos que deixamos inalterada a ordem de força das combinações: as trincas são superiores a dois pares. Neste caso, sempre que recebemos um curinga, um pocket pair e duas outras cartas, usamos o joker para fortalecer a nossa mão para trincas.
Sem o curinga, as trincas poderiam aparecer 54.912 vezes. Por causa do Curinga, seu número aumentou para 137.280.
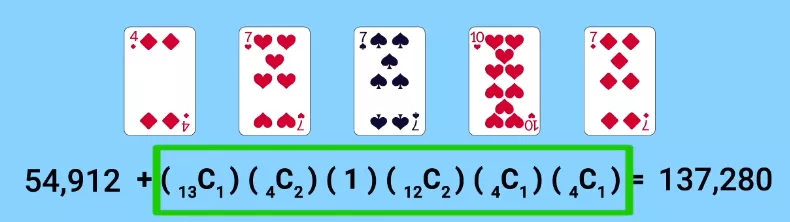
Mas isto é mais do que o número de combinações possíveis de dois pares! Eram 123.552 sem curinga, e esse número não mudou após a introdução de uma carta adicional, pois sempre que temos a oportunidade de fazer dois pares com ela, preferimos trincas, e dois pares com curinga sempre se transformam em um full house.
Como agora dois pares são encontrados com menos frequência do que trincas, a ordem das combinações deve ser alterada. Mas então torna-se inútil para os jogadores fazer trincas usando curingas! O número de trincas volta aos 54.912 originais e o número de combinações de dois pares aumenta para 205.920.
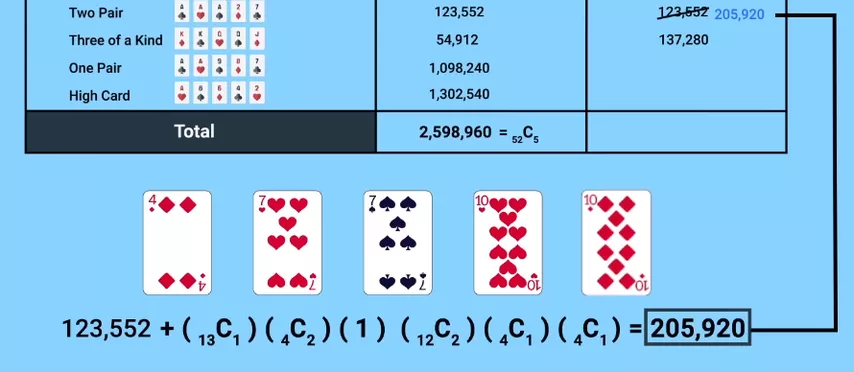
Surge um ciclo interminável e chegamos a um paradoxo: torna-se impossível escolher a combinação mais alta com base na probabilidade de sua ocorrência.
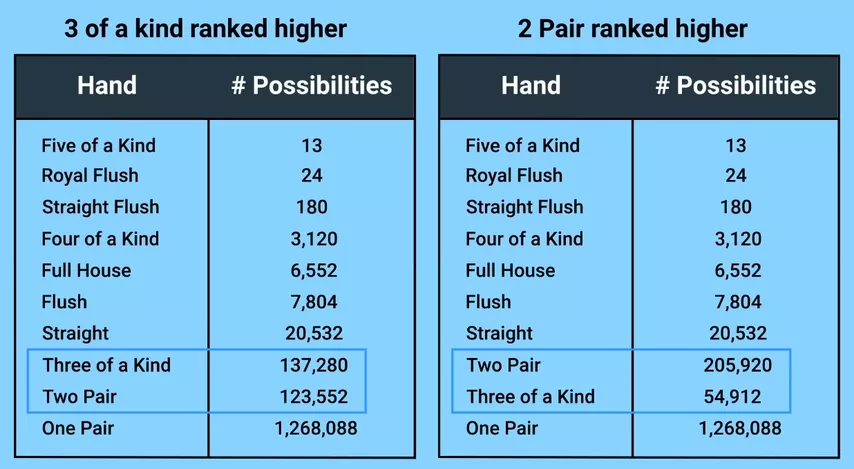
Se você estiver interessado, aqui estão as probabilidades de combinações ao jogar com um curinga:
- Aumento do bônus de primeiro depósito
- Aumento de rakeback e em bônus
- Ajuda com depósitos e saques
- Acesso a freerolls exclusivos
- Suporte 24 horas por dia, 7 dias por semana
Um jogo quase justo
Vou mostrar-lhe um jogo que à primeira vista parece bastante justo, mas graças a um algoritmo simples permitirá que você ganhe pelo menos duas vezes em três, e em condições favoráveis – mais de sete vezes para uma.
Jogamos com um baralho normal de 52 cartas, metade das quais são pretas e a outra metade são vermelhas. Dois jogadores participam. O primeiro seleciona uma sequência de três cartas, nomeando sua cor, por exemplo, “vermelho – vermelho – preto”. Então o segundo jogador faz o mesmo. Depois disso, eles começam a retirar cartas do baralho, e aquele cuja sequência sair primeiro vence.
Parece não haver problema. Bem-vindo ao jogo Humble-Nishiyama!
Em outubro de 1969, Walter Penny publicou um jogo simples de lançamento de moeda no Journal of Recreational Mathematics. Logo Steve Humble e Yutaka Nishiyama adaptaram o jogo para um baralho de cartas padrão.
Que armadilhas podem existir? Bem, você provavelmente não deveria escolher uma sequência de três cartas idênticas, porque a probabilidade de ver um terceira carta vermelho depois de dois vermelhos já terem saído é ligeiramente reduzida. Mas o que mais? Afinal, a chance de obter uma carta preta ou vermelha é sempre de 50/50.
Na verdade, se excluirmos as opções de uma únicacora de VVV e PPP, praticamente não há diferença para o primeiro jogador a escolher. Porém, o segundo tem uma estratégia que garante a vitória.
Digamos que o primeiro jogador escolheu o PVP. Pegamos a segunda carta de sua sequência, mudamos a cor, colocamos no início, retiramos a última carta – e o ajuste está pronto:
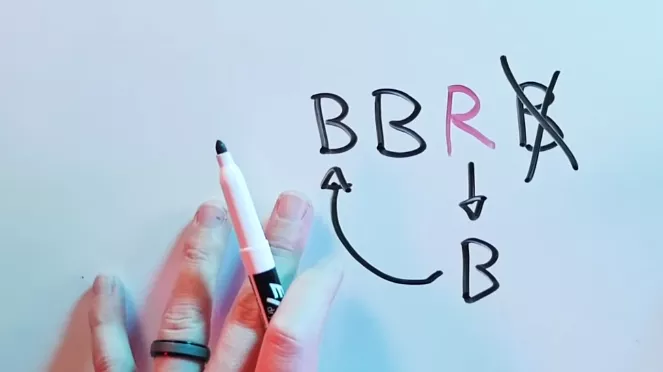
Nossa vantagem sobre o primeiro jogador é mais convincente do que a diversão inocente da distribuição aleatória de cartas pode sugerir:
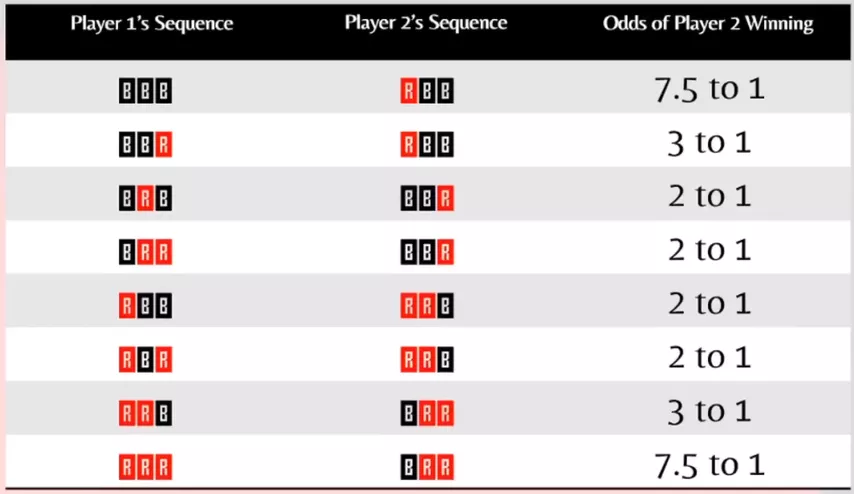
E existe o porquê este jogo pertence à classe dos intransitivos.
Exemplo de transitividade:
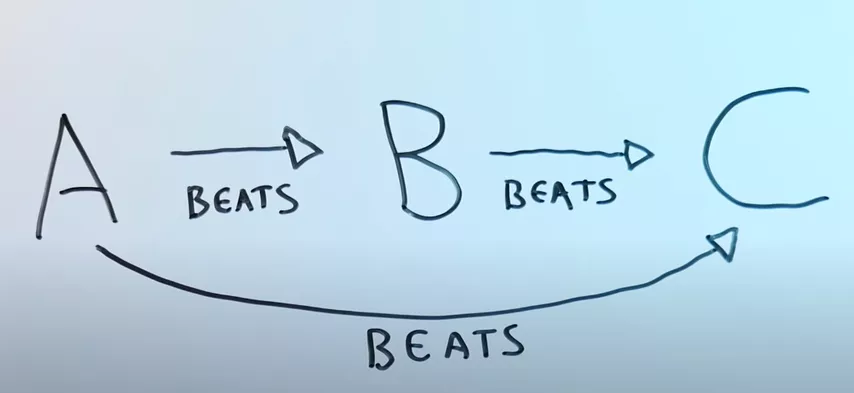
Se você gosta mais de pizza do que de tacos e prefere tacos à ração enlatada para cachorro, ao escolher entre pizza e ração enlatada para cachorro, você também votará em pizza. Essas preferências alimentares serão transitivas. No entanto, se por alguma razão desconhecida a comida de cachorro for mais saborosa para você do que pizza (mas apenas neste par!), suas preferências alimentares serão intransitivas.
Em jogos não transitivos, o primeiro jogador não tem a escolha melhor. As relações neles descrevem preferências em pares de alternativas, cuja comparação leva à presença de ciclos: A é preferível a B, B é preferível a C e C é preferível a A. O exemplo clássico é, claro, pedra, papel, tesoura. Este jogo cria um ciclo de escolhas possíveis, nenhuma das quais oferece a melhor chance de vitória.
O jogo Humble-Nishiyama também é intransitivo. Aqui está a hierarquia de loops neste jogo:
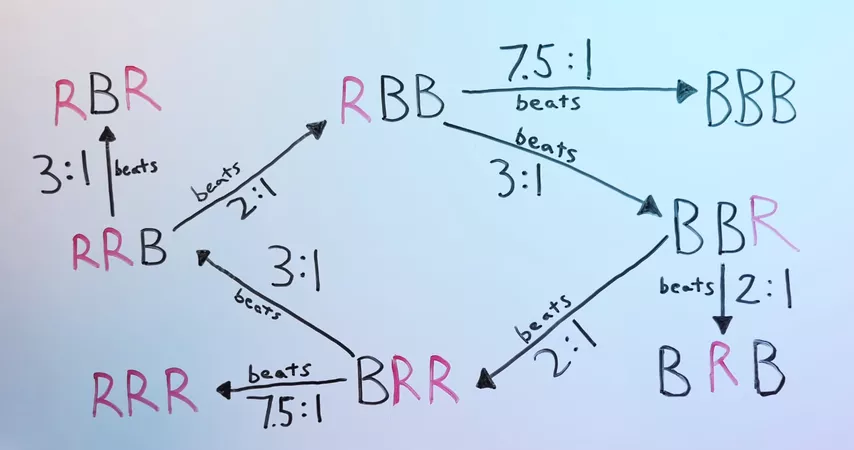
Conhecendo a escolha do primeiro jogador, podemos escolher a sequência mais lucrativa. E o jogo, que à primeira vista parecia tão justo, na verdade dá ao segundo jogador uma enorme vantagem.












